一、填空题(共32分)
1.(本题4分)4.8立方米=(______)立方分米 700毫升=(______)升
7.8米=(______)厘米 3时12分=(______)时。
2.(本题3分)一个圆柱体,如果把它的高截短3厘米,表面积就减少94.2cm2,体积减少了它的 立方厘米.
3.(本题3分)等底等高的圆锥体积和圆柱体积比的比值是____。
4.(本题3分)一个圆柱的底面半径是2 cm,高是5 cm,它的侧面积是(_______),表面积是(______),体积是(______).
5.(本题3分)一个圆柱的侧面展开图是一个正方形,这个圆柱的高是,那么圆柱的底面周长是(________),底面直径是(________)。
6.(本题6分)等底等高的圆柱和圆锥的体积相差24m3,这个圆柱的体积是(______)m3,圆锥的体积是(______)m3。
7.(本题3分)一个圆锥比一个与它等底等高的圆柱的体积少16cm3,这个圆锥的体积是__。
8.(本题4分)请你制作一个无盖的圆柱形水桶,有以下几种型号的铁皮供选择。
①你选择的材料是(________)号和(________)号。
②你选择的材料制成的水桶的容积是(________)升。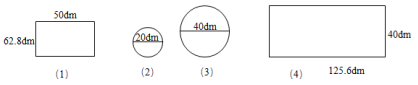
9.(本题3分)一个圆锥和一个圆柱等底等高,圆锥的体积是32立方厘米,圆柱的体积是(______)立方厘米。
二、判断题(共10分)
10.(本题2分)如果两个圆柱底面半径相等,那么它们的表面积也一定相等。(______)11.(本题2分)一个圆柱削成一个与它等底等高的圆锥, 削去的部分是圆锥的200%.(______)
12.(本题2分)两个圆柱的底面积相等,那么它们的侧面积也一定相等。(______)
13.(本题2分)一个圆锥和圆柱体等底等高,圆锥与圆柱体的体积比是1:3 。 (______)
14.(本题2分)一个圆锥,体积是10.2立方米﹐底面积是3.4平方米,求高是多少。算式是:10.2÷3.4÷3。(______)
三、选择题(共10分)
15.(本题2分)两个圆柱的底面周长相等,则它们的( )相等。
A.侧面积 B.表面积 C.底面积 D.体积
16.(本题2分)将一个3厘米长的圆柱截成三段后,表面积增加了12.56平方厘米,这个圆柱原来的体积是( )立方厘米。
A.12.56 B.9.42 C.18.84 D.18.9
17.(本题2分)一个圆锥的体积是3立方米,底面积是9平方米,它的高是( )。
A.1米 B.1/3米 C.3米 D.9米
18.(本题2分)已知圆柱侧面(如图,单位:厘米),选一个合适的底面制作容积最大的圆柱体形易拉罐,这个底面周长应是( )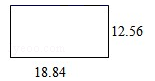
A.18.84厘米 B.12.56厘米 C.4厘米 D.6厘米
19.(本题2分)一个圆锥体与一个圆柱体的底面积相等,圆锥体的高是圆柱体的6倍,圆柱体的体积是圆锥体的( )
A.2倍 B.1/6 C.1/2 D.1/3
四、计算题(共9分)
20.(本题9分)计算下面各图形的体积。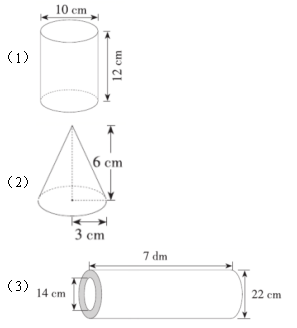
五、解答题(共39分)
21.(本题6分)一个圆柱体和一个长方体高相等,它们底面积的比是5:3.已知圆柱的体积是80立方分米,长方体的体积比圆柱体少多少立方分米?
22.(本题6分)用彩带捆扎一个圆柱形的蛋糕盒(如下图),底面直径是40厘米、高是20厘米,打结处用去的彩带长10厘米。扎这个盒子至少用去彩带多少厘米?若要在它的整个侧面贴上商标,商标的面积至少多少平方厘米?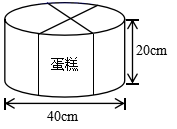
23.(本题6分)一个圆柱形的玻璃杯,底面直径为20厘米,水深24厘米,当放入一个底面直径是6厘米的圆锥形铁块后,水深24.6厘米.圆锥形铁块的高是多少厘米?
24.(本题6分)一个圆柱形水池,从里面量水池底面直径是6m,池深1.2m。如果在水池内壁和底面都抹上水泥,抹水泥的面积是多少m2?
25.(本题6分)一个圆柱的高是8厘米,侧面积是251.2平方厘米,它的体积是多少?
26.(本题9分)两位同学用硬纸各做了一面小旗.单位:厘米.
(1) 制作的小旗用的材料多.
(2)想象一下:乐乐的小旗快速旋转后得到的图形是 ;淘淘的小旗快速旋转后得到的图形是
(3)求出乐乐的小旗快速旋转后得到的图形的表面积.
参考答案
1.4800 0.7 780 3.2
【详解】
试题分析:(1)把4.8立方米换算成立方分米数,用4.8乘进率1000得4800立方分米;
(2)把700毫升换算成升数,用700除以进率1000得0.7升;
(3)把7.8米换算成厘米数,用7.8乘进率100得780厘米;
(4)把3时12分换算成时数,先把12分换算成时数,用12除以进率60得0.2时,再加上3时得3.2时。
解:(1)4.8立方米=4800立方分米;
(2)700毫升=0.7升;
(3)7.8米=780厘米;
(4)3时12分=3.2时。
故答案为4800,0.7,780,3.2.
点评:此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率;把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
2.235.5.
【解析】
试题分析:根据题干可知,减少部分面积是高为3厘米的圆柱部分的侧面积,根据侧面积=底面周长×高即可求出底面半径,利用V=Sh即可解决问题.
解:圆柱的底面周长为:94.2÷3=31.4(厘米),
则半径为:31.4÷3.14÷2=5(厘米),
那么减少部分的体积为:
3.14×52×3
=3.14×25×3
=235.5(立方厘米),
答:体积减少了235.5立方厘米.
故答案为235.5.
点评:此题考查了圆柱的表面积和体积公式的应用,抓住减少部分的表面积是截去部分的侧面积,即可解决问题.
3.1/3
【分析】
根据等底等高的圆锥体积是圆柱体积的1/3。
【详解】
因为根据等底等高的圆锥体积是圆柱体积的。
所以V锥:V柱=1:3=1/3
【点睛】
一定要注意只有等底等高的圆锥体积是圆柱体积的1/3,“等底等高。”这个条件是基本前提。
4.62.8cm2 87.92cm2 62.8cm3
【解析】
略
5.25.12 8
【分析】
由题意可知,圆柱的侧面展开图是一个正方形,所以圆柱的底面周长等于圆柱的高,即圆柱的底面周长为,再根据“d=c÷π”求出直径即可。
【详解】
圆柱的底面周长为;
25.12÷3.14=8(分米)。
【点睛】
明确圆柱的侧面展开图是一个正方形时,圆柱的底面周长和高相等是解答本题的关键。
6.36 12
【分析】
根据等底等高的圆柱的体积是圆锥的体积的3倍,知道等底等高的圆柱的体积与圆锥的体积相差(3-1)倍,由此用24除以(3-1)就是圆锥的体积,进而求出圆柱的体积。
【详解】
24÷(3-1)
=24÷2
=12(立方米)
12×3=36(立方米)
故答案为:36;12
【点睛】
本题主要利用等底等高的圆柱的体积与圆锥的体积的关系解决问题。
7.8立方厘米
【分析】
因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的(3-1)倍,根据已知一个数的几倍是多少,求这个数,用除法解答。
【详解】
16÷(3-1)
=16÷2
=8(立方厘米)
故答案为:8立方厘米。
【点睛】
明确圆柱的体积是与它等底等高的圆锥的体积的3倍是解决本题的关键。
8.(1) (2) 15700
【分析】
(1)由圆柱的侧面展开图的特点可知:圆柱的侧面展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,据此即可计算长方形的长与圆形的底面周长,若相等,则可以选择,否则不能选择;
(2)求水桶的容积可以利用圆柱的体积公式,即圆柱的体积=底面积×高,将两组数据分别代入公式即可求其容积。
【详解】
①因为(2)号的周长是:3.14×20=62.8(分米),
等于(1)号的长,所以可以选(1)号和(2)号搭配;
②(1)号和(2)号制作的水桶的容积是:
3.14×(20÷2)2×50
=3.14×100×50
=314×50
=15700(立方分米)
=15700(升)
【点睛】
解答此题的关键是明白:长方形的长与圆形的底面周长,若相等,则可以选择,否则不能选择。
9.96
【分析】
等底等高的圆柱是圆锥的体积的3倍,由此计算可求圆柱的体积即可求解。
【详解】
32×3=96(立方厘米)
答:圆柱的体积是96立方厘米。
故答案为:96。
【点睛】
此题考查了等底等高的圆柱与圆锥的体积关系的灵活应用。
10.×
【分析】
要判断对或错,要通过圆柱的表面积的计算公式进行分析,进而比较得出结论。
【详解】
根据圆柱的表面积=底面积+侧面积=πr2×2+2πrh,
圆柱的表面积不但和半径有关,而且与高有关;所以说法不对。
故答案为×。
【点睛】
此题一定要结合圆柱的表面积计算公式进行分析、比较,进而得出问题答案。
11.√
【详解】
略
12.×
【分析】
因为两个圆柱的底面积相等,所以两个圆柱的底面半径和周长相等。又因为圆柱的侧面积=底面周长×高,虽然两个圆柱的底面周长相等,但是两个圆柱的高不一定相等,所以侧面积不一定相等。
【详解】
两个圆柱的底面积相等,因为高不一定相等,那么它们的侧面积也不一定相等。
故答案为:×
【点睛】
本题的关键是两个圆柱底面周长虽然相等,但是圆柱的高不一定相等。
13.√
【解析】
【详解】
略
14.×
【分析】
圆锥的体积=1/3×底面积×高,可用圆锥的体积除以底面积再除以1/3即可得到圆锥的高。
【详解】
10.2÷3.4÷1/3
故答案为:×
【点睛】
此题主要考查圆锥体积公式的灵活应用,学生应掌握。
15.C
【分析】
两个圆柱的底面周长相等,也就是圆的周长相等,根据圆的周长公式C=2r可得,半径也相等,根据圆的面积公式可得体积也相等。
【详解】
圆柱的底面半径=圆柱底面周长÷÷2
圆柱底面积=×半径×半径
所以,它们的底面积相等。
故选:C
【点睛】
此题考查的是圆柱的底面周长和底面积都只和底面半径有关。
16.B
【分析】
圆柱截成三段后,增加了4个底面,先求出底面积,圆柱的长就是高,用底面积×高即可。
【详解】
12.56÷4×3
=3.14×3
=9.42(立方厘米)
故答案为:B
【点睛】
关键是先求出底面积,熟练运用圆柱体积公式。
17.A
【分析】
圆锥的高=圆锥的体积×3÷底面积,把数据带入公式解答即可。
【详解】
3×3÷9
=9÷9
=1(m)
故答案为:A
【点睛】
灵活运用圆锥体积公式是解决此题的关键。
18.A
【解析】
试题分析:抓住“最大”,就是制作成以这个长方形为侧面的圆柱,即可选出正确答案.
解:圆柱体侧面展开图的特点,这个长方形的长就是底面的周长,而且,
A:底面周长为18.84时,r=18.84÷3.14÷2=6÷2=3厘米,
V=Sh=3.14×32×12.56=3.14×9×12.56=354.9456立方厘米;
B:底面周长为12.56时,r=12.56÷3.14÷2=4÷2=2厘米,
V=Sh=3.14×22×12.56=3.14×4×12.56=157.7536立方厘米;
C和D的底面半径更小,所以它们的体积更小,
所以这个底面周长应该是18.84厘米;
故选A.
点评:此题考查了圆柱体展开图的特点的应用.
19.B
【解析】
试题分析:由题意可得:圆柱的底面积=圆锥的底面积,圆锥的高等于圆柱的6倍,所以可设圆柱的高为h,则圆锥的高为6h,把它代入圆柱、圆锥的体积公式,然后再用圆柱的体积除以圆锥的体积即可.
解:设圆柱的底面积为s,高为h,则圆锥的高为6h,
圆柱的体积=sh,
圆锥的体积为:6sh,
所以sh÷6sh=1/6,
答:圆柱的体积是圆锥体积的1/6倍.
故选B.
点评:此题是考查圆柱、圆锥的关系,可利用圆柱、圆锥的体积公式解答.
20.(1)942cm3;(2)56.52cm3;(3)15825.6cm3
【分析】
(1)根据圆柱的体积公式:V柱=πr2h,代入数据解答即可。
(2)根据圆锥的体积公式:V锥=1/3πr2h,代入数据解答即可。
(3)先用S圆环=π(R2-r2)计算出圆环的面积,再用圆环的面积乘长,注意单位的统一。
【详解】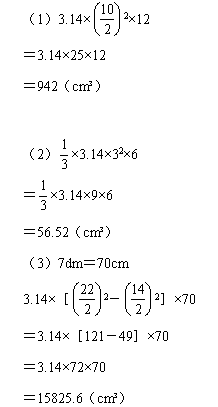
【点睛】
熟练运用圆柱和圆锥的体积公式细心计算,注意单位的统一。
21.32立方分米.
【解析】
试题分析:因为圆柱体与长方体的体积都等于底面积×高,所以高一定时,它们的底面积与体积成正比例,据此可得圆柱体的体积与长方体的体积之比是5:3,设长方体的体积是x立方分米,可得:80:x=5:3,据此即可求出长方体的体积,再与圆柱体的体积相减即可.
解:设长方体的体积是x立方分米,可得:
80:x=5:3,
5x=80×3,
x=48,
80﹣48=32(立方分米),
答:长方体的体积比圆柱体的体积少32立方分米.
点评:解答此题的关键是明确高一定时,圆柱体与长方体的体积与它们的底面积成正比例的性质.
22.250厘米;2512平方厘米
【分析】
看图可知,彩带长度=直径×4+20×4+打结处长度;根据圆柱侧面积=底面周长×高,列式解答即可。
【详解】
40×4+20×4+10
=160+80+10
=250(厘米)
3.14×40×20=2512(平方厘米)
答:扎这个盒子至少用去彩带250厘米,若要在它的整个侧面贴上商标,商标的面积至少2512平方厘米。
【点睛】
关键是熟悉圆柱特征,掌握圆柱侧面积公式。
23.20厘米
【解析】
试题分析:根据题干得出,这个圆锥形铁块的体积就是上升24.6﹣24=0.6(厘米)的水的体积,由此可以求出这个圆锥的体积,再利用圆锥的体积公式即可求出这个圆锥的高.
解:圆锥铁块的体积:3.14×(20÷2)2×(24.6﹣24),
=3.14×100×0.6,
=314×0.6,
=188.4(立方厘米),
铁块的高:188.4×3÷[3.14×(6÷2)2],
=188.4×3÷[3.14×9],
=565.2÷28.26,
=20(厘米),
答:圆锥形铁块的高是20厘米.
点评:此题考查了圆柱与圆锥的体积公式的灵活应用,这里根据上升的水的体积求得圆锥铁块的体积是本题的关键.
24.50.868m2
【分析】
分析题意,抹水泥的部分为圆柱的底面和侧面,据此结合圆柱的表面积公式求出抹水泥的面积即可。
【详解】
3.14×(6÷2)2+3.14×6×1.2
=28.26+22.608
=50.868(m2)
答:抹水泥的面积是50.868m2。
【点睛】
本题考查了圆柱的表面积应用,灵活运用圆柱的表面积公式是解题的关键。
25.628立方厘米
【解析】
试题分析:是根据圆柱的侧面积公式:s=ch,求出底面周长,进而求出底面半径,再根据圆柱的体积公式:v=sh,比实际代入公式解答.
解:底面周长:251.2÷8=31.4(厘米),
底面半径:31.4÷3.14÷2=5(厘米),
体积:3.14×52×8,
=3.14×25×8,
=78.5×8,
=628(立方厘米);
答:它的体积是628立方厘米.
点评:此题主要考查圆柱的侧面积公式、体积公式的综合运用.
26.乐乐;圆柱、圆锥
【解析】
试题分析:(1)根据长方形的面积公式S=ab,求出乐乐做小旗用的材料的面积,再根据三角形的面积公式S=ah÷2,求出淘淘做小旗用的材料的面积,再做比较即可;
(2)乐乐的小旗快速旋转后得到的图形是圆柱;淘淘的小旗快速旋转后得到的图形是圆锥;
(3)求乐乐的小旗快速旋转后得到的图形的表面积,实际是求底面半径是20厘米,高是8厘米的圆柱的表面积,根据圆柱的表面积的就是方法:2个底面积+侧面积,列式解答即可.
解:(1)乐乐小旗的面积:20×8=160(平方厘米),
淘淘小旗的面积:20×15÷2=150(平方厘米),
160>150,
所以乐乐制作的小旗用的材料多,
(2)乐乐的小旗快速旋转后得到的图形是圆柱;淘淘的小旗快速旋转后得到的图形是圆锥;
(3)2×3.14×202+2×3.14×20×8,
=6.28×400+6.28×160,
=6.28×(400+160),
=6.28×560,
=3516.8(平方厘米);
答:乐乐的小旗快速旋转后得到的图形的表面积是3516.8平方厘米.
故答案为乐乐;圆柱、圆锥.
点评:关键是根据题目中不同的要求,运用相应的公式解决问题.
注:需打印的家长,请自行将内容复制到word里进行打印!(试卷来源:https://appsj.szxuexiao.com/html/6154.html)