一、填空题(共8题;共16分)
1.一个比例中,两个内项分别是10和 4/5,其中一个外项是4.5,另一个外项是________。
2.如果向东走100米记作+100米,那么向西走50米记作________米。
3.大圆的直径是4厘米,小圆的直径是2厘米,大圆和小圆面积最简单的整数比是________:________。
4.在一个比例中,两个外项互为倒数,其中一个内项是 1/6,则另一个内项是________。
5.下边的比例尺表示图上1厘米相当于地面实际距离________千米,把它改写成数值比例尺是________∶________。 
6.一个圆锥形状的沙石堆,底面积12.56平方米,高1.2米.如果用这堆沙石铺路,公路宽10米,沙石厚0.2米,能铺________米长?
7.将底面周长6.28分米,高20厘米的圆柱沿直径切开,则表面积增加________平方厘米。
8.三角形的面积一定,它的底和高成________比例。
二、判断题(共5题;共10分)
1.圆柱的表面积可以用公式S=2πr×(r+h)来计算。 ( )
2.0既不是正数也不是负数.( )
3.把一个比的前项扩大2倍,后项缩小到原来的 ,这个比的比值不变。( )
4.甲、乙两个圆柱的体积相等,如果甲圆柱的高是乙圆柱的 ,那么甲圆柱的半径则是乙圆柱的1.5倍。( )
5.汽车的速度一定,所行路程和时间成正比例。( )
三、单选题(共6题;共12分)
1.已知 B/5=3/A ,那么A和B( )。
A.成反比例 B.成正比例 C.不成比例 D.无法确定
2.圆锥的底面半径扩大2倍,高扩大2倍,体积扩大( )倍。
A.2 B.4 C.8 D.16
3.做同样的衬衫,做的件数与用布米数( )
A. 成正比例 B. 成反比例 C. 不成比例 D. 不成正比例
4.下面图( )表示的是成正比例关系的图像。 
5.体积是( ) 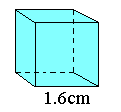
A.0.64 cm3 B.4.096 cm3 C.0.512 cm3 D.2.56 cm3
6.甲书柜的书与乙书柜的书的比为11:13,从乙书柜拿20本书放到甲书柜后,两书柜书的数量相同,则甲书柜与乙书柜原来各有( )本书.
A. 220、260 B. 260、220 C. 120、160 D. 160、120
四、计算题(共2题;共24分)
1.直接写出得数。 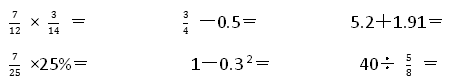
2.解方程。
①7x+7.2=10 ②18+1.5x=21 ③10x+85=310
④2x+6.4=16.4 ⑤0.21x+0.63=4.2 ⑥7x÷3=63
五、计算下面图形面积。(共2题;共10分)
1.计算下面圆柱的表面积和体积。(单位:厘米,π=3.14) 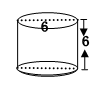
2.计算下面圆锥体的体积。(单位:厘米,π=3.14) 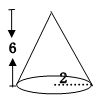
六、应用题(共6题;共30分)
1.王萍家购买了一套新房,总价60万元。按规定,王萍家还要按购房总价的2%缴纳契税,按购房总价的0.03%缴纳印花税。她家一共要缴纳多少万元税费?
2.一个粮仓装满稻谷后上半部分是圆锥形,下半部分是圆柱形。粮仓的底面周长是18.84米,圆柱高2米,圆锥高0.6米。如果每立方米稻谷重600千克,那么这个粮仓装有多少千克稻谷?
3.小明看一本故事书,计划每天看20页,18天看完,实际每天看30页,实际多少天看完?
4.把一个铁块浸没在一个底面半径是6厘米,水深20厘米的圆柱形容器中,水面上升到22厘米,且水未溢出,这个铁块的体积是多少立方厘米?
5.给一间房子铺地,如果用边长6分米的方砖,需要80块。如果改用边长8分米的方砖,需要多少块?
6.有一个近似圆锥形的小麦堆,测得麦堆底面直径4米,高1.5米,如果每立方米小麦重740千克,这堆小麦大约重多少千克?
参考答案
一、填空题
1. 1 7/9
【考点】比例的基本性质 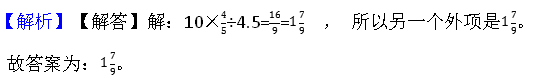
【分析】比例的基本性质:在比例里,两内项的积等于两外项的积,据此作答即可。
2. -50
【考点】正、负数的意义与应用
【解析】【解答】解:如果向东走100米记作+100米,那么向西走50米记作-50米。
故答案为:-50。
【分析】正负数表示一组相反意义的量,向东走记作正,那么向西走就记作负。
3. 4;1
【考点】圆的面积,比的应用 
4. 6
【考点】倒数的认识,比例的基本性质
【解析】【解答】解:另一个内项是1÷1/6=6。
故答案为:6。
【分析】在比例里,两个内项积等于两个外项的积。两个外项互为倒数,则两个内项也互为倒数,所以用1除以已知的内项即可求出未知的内项。
5. 20;1;2000000
【考点】比例尺的认识
【解析】【解答】解:这个比例尺表示图上1厘米相当于地面实际距离20千米;改写成数值比例尺是1厘米:20千米=1厘米:2000000厘米=1:2000000。
故答案为:20;1;2000000。
【分析】线段比例尺中1厘米相当于20千米,把20千米换算成厘米,然后写出图上距离与实际距离的比即可改写成数值比例尺。
6. 2.512
【考点】长方体和正方体的体积,圆锥的体积(容积)
【解析】【解答】解:12.56×1.2×1/3÷(10×0.2)
=5.024÷2
=2.512(米)
故答案为:2.512
【分析】圆锥的体积=底面积×高×1/3,长方体的体积=长×宽×高,根据圆锥的体积公式求出砂石堆的体积,然后用砂石堆的体积除以公路的宽和厚度的积即可求出能铺的长度.
7. 800
【考点】圆柱的侧面积、表面积,立方体的切拼
【解析】【解答】解:6.28分米=62.8厘米,底面直径:62.8÷3.14=20(厘米);表面积增加:20×20×2=800(平方厘米)。
故答案为:800。
【分析】表面积增加的是两个相同的切面(长方形或正方形),切面的一条边与圆柱的高相等,另一条边与圆柱的底面直径相等。用底面周长除以3.14求出底面直径,再用底面直径乘高求出一个切面的面积,再乘2就是表面积增加的面积。
8.反
【考点】成反比例的量及其意义
【解析】【解答】因为1/2×底×高=三角形的面积(一定),所以三角形的面积一定,它的底和高成反比例.
故答案为:反.
【分析】正比例关系式是:=k(一定),反比例关系式:xy=k(一定),判断两种相关联的量成什么比例关系,就看这两种量是对应的比值一定还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,否则,不成比例,据此根据三角形的面积公式分析解答.
二、判断题
1. 正确
【考点】圆柱的侧面积、表面积
【解析】【解答】解:S=2πrr+2πrh=2πr×(r+h),原题说法正确。
故答案为:正确。
【分析】圆柱的表面积=底面积×2+侧面积,圆柱的侧面积=底面周长×高,由此写出公式并化简即可做出判断。
2. 正确
【考点】正、负数的意义与应用
【解析】【解答】解:整数包括正整数、负整数和0;
所以,0既不是正数也不是负数是对的;
故答案为:正确.
【分析】整数包括正整数、负整数和0.此题考查了整数包括正整数、负整数和0.
3. 错误
【考点】比的基本性质
【解析】【解答】解:一个比的前项扩大2倍,后项缩小到原来的 , 这个比的比值会扩大到原来的4倍。原题说法错误。
故答案为:错误。
【分析】一个比的前项扩大2倍,比值会扩大2倍;后项缩小到原来的 , 比值又会扩大2倍;比值一共扩大4倍。
4. 正确
【考点】圆的面积,圆柱的体积(容积)
【解析】【解答】解:因为体积相等,那么甲圆柱的底面积是乙圆柱的9/4倍,因为3/2 x 3/2 = 9/4, 所以甲圆柱的半径是乙圆柱的1.5倍。原题说法正确。
故答案为:正确。
【分析】圆柱的体积=底面积×高,所以甲圆柱的底面积是乙圆柱的9/4倍。根据圆面积公式判断半径的倍数关系即可。
5. 正确
【考点】成正比例的量及其意义
【解析】【解答】解:路程÷时间=速度,速度一定,路程和时间的商一定,二者成正比例。原题说法正确。
故答案为:正确。
【分析】根据数量关系判断路程与时间的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
三、单选题
1. A
【考点】成反比例的量及其意义
【解析】【解答】解:因为B/5 = 3/A, 所以AB=5×3,A、B的乘积一定,二者成反比例。
故答案为:A。
【分析】根据比例的基本性质把比例写成两个内项积等于两个外项积的形式,这样就能确定A、B的乘积一定,由此选择即可。
2. C
【考点】圆锥的体积(容积)
【解析】【解答】解:体积扩大的倍数:2×2×2=8。
故答案为:C。
【分析】圆锥的底面半径扩大2倍,底面积就会扩大(2×2)倍,高扩大2倍,则体积就会扩大(2×2×2)倍,由此计算即可。
3. A
【考点】成正比例的量及其意义
【解析】【解答】解:用布的米数÷做的件数=每件衬衫用布的长度,因为衬衫一样,所以每件衬衫用布的长度一定,用布的米数与做的件数的商一定,二者成正比例.
故答案为:A
【分析】根据数量关系判断用布的米数与做的件数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
4. C
【考点】成正比例的量及其意义
【解析】【解答】解:只有C图中线是一条射线且经过原点,所以图C表示的是成正比例关系的图像。
故答案为:C。
【分析】成正比例关系的两个量的比值一定,成正比例关系的图像是一条经过原点的射线,由此判断并选择即可。
5.B
【考点】正方体的体积
【解析】【解答】解:1.6×1.6×1.6=4.096(cm3)
故答案为:B。
【分析】正方体体积=棱长×棱长×棱长,由此根据公式计算体积即可。
6.A
【考点】比的应用
【解析】【解答】解:把甲书柜书的本数看作11份数,乙书柜书的本数看作13份数,那么乙书柜的书就比甲书柜多13﹣11=2份数 20×2÷2=20(本)
甲书柜原有:20×11=220(本)
乙书柜原有:20×13=260(本).
答:甲书柜原有220本书,乙书柜原有260本书.
故选:A.
【分析】根据题意,把甲书柜书的本数看作11份数,乙书柜书的本数看作13份数,那么乙书柜的书就比甲书柜多13﹣11=2份数;再根据“从乙书柜拿20本书放到甲书柜后,两书柜书的数量相同”,可知原来乙书柜的书比甲书柜多20×2=40本;进而先求得每一份数,再进一步计算问题得解.
四、计算题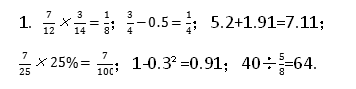
【考点】分数与分数相乘,除数是分数的分数除法,百分数与分数的互化
【解析】【分析】计算分数乘法时能约分的要先约分再乘;计算分数除法时要把除法转化成乘法;计算小数加减法时要注意小数点的位置;计算分数、百分数和小数的混合运算时要先统一再计算。
2.①7x+7.2=10
7x=10-7.2
7x=2.8
x=2.8÷7
x=0.4
②18+1.5x=21
1.5x=21-18
1.5x=3
x=3÷1.5
x=2
③10x+85=310
10x=310-85
10x=225
x=225÷10
x=22.5
④2x+6.4=16.4
2x=16.4-6.4
2x=10
x=10÷2
x=5
⑤0.21x+0.63=4.2
0.21x=4.2-0.63
0.21x=3.57
x=3.57÷0.21
x=17
⑥7x÷3=63
7x=63×3
7x=189
x=189÷7
x=27
【考点】综合应用等式的性质解方程
【解析】【分析】解方程的一般步骤:1.有括号就先去括号,也可将括号中内容看作一个整体先参与计算;2.将含未知数的项移到等式左边,常数项移到等式右边;3.合并同类项,化简方程;4.方程两边同时除以一个相同的数(未知数前面的数),得到未知数的解。
五、计算下面图形面积。
1. 解:表面积:
3.14×(6÷2)2×2+3.14×6×6
=3.14×18+3.14×36
=56.52+113.04
=169.56(平方厘米)
体积:3.14×(6÷2)2×6
=3.14×9×6
=169.54(立方厘米)
【考点】圆柱的侧面积、表面积,圆柱的体积(容积)
【解析】【分析】圆柱的表面积=底面积×2+侧面积,圆柱的侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式分别计算即可。
2. 解:3.14×22×6×1/3
=3.14×4×2
=25.12(立方厘米)
【考点】圆锥的体积(容积)
【解析】【分析】圆锥的体积=底面积×高×1/3, 由此根据公式计算体积即可。
六、应用题
1. 解:60×2%+60×0.03%=1.218(万元)
【考点】百分数的应用--税率
【解析】【解答】 60×2%+60×0.03%
=1.2+0.018
=1.218(万元)
答:她家一共要缴纳1.218万元税费.
【分析】根据题意可知,王萍购买一套新房,需要交契税和印花税,用购房总价×契税的税率=缴纳的契税金额,购房总价×印花税的税率=缴纳的印花税金额,然后把两种缴税金额相加即可解答.
2. 解:圆锥和圆柱姆面积桓,,为:3·14×(18·84÷3.14÷2)2=28.26(平方米),所以圆锥和圆柱的总体积(即粮仓的总容积)为:1/3×28.26×0.6+28.26×2=62.172(立方米),稻谷的质量为:600×62.172=37303.2(千克)。
【考点】圆柱的体积(容积),圆锥的体积(容积)
【解析】【解答】答:这个粮仓装油37303.2千克稻谷。
【分析】圆柱和圆锥的底面相等,用底面周长除以3.14再除以2求出底面半径,再根据圆面积公式计算底面积;圆柱的体积=底面积×高,圆锥的体积=底面积×高×1/3, 根据公式计算出体积的和就是装稻谷的体积,再乘每立方米稻谷的重量即可求出装稻谷的总重量。
3. 解:20x18÷30=12(天)
【考点】反比例应用题
【解析】【解答】解:设实际x天看完。
30x=20×18
x=360÷30
x=12
答:实际12天看完。
【分析】总页数不变,每天看的页数和看的天数的乘积一定,二者成反比例;先设出未知数,根据总页数不变列出比例,解比例求出实际看完的天数。
4.解:3.14×62×(22-20)
=3.14×36×2
=226.08(立方厘米)
答:这个铁块的体积是226.08立方厘米。
【考点】圆柱的体积(容积),不规则物体的体积算法
【解析】【解答】 3.14×62×(22-20)
=3.14×62×2
=3.14×36×2
=113.04×2
=226.08(立方厘米)
答:这个铁块的体积是226.08立方厘米。
【分析】根据题意可知,水面上升部分的体积就是铁块的体积,用圆柱的底面积×水面上升部分的高度=铁块的体积,据此列式解答.
5. 解:设需要x块。
(8×8)x=6×6×80
64x=2880
x=2880÷64
x=45
答:需要45块。
【考点】反比例应用题
【解析】【分析】每块方砖的面积×方砖的块数=房间的面积,每块方砖的面积与方砖的块数成反比例;设出未知数,根据总面积不变列出比例,解比例求出需要方砖的块数即可。
6. 解:3.14×(4÷2)2×1.5×1/3×740
=3.14×4×0.5×740
=3.14×1480
=4647.2(千克)
答:这堆小麦约重4647.2千克。
【考点】圆锥的体积(容积)
【解析】【分析】圆锥的体积=底面积×高×1/3, 根据公式计算出小麦的体积,再乘每立方米小麦的重量即可求出总重量。
注:需打印的家长,请自行将内容复制到word里进行打印!(转载请注明出处<深圳学校网>,文章来源:https://appsj.szxuexiao.com/html/5902.html)